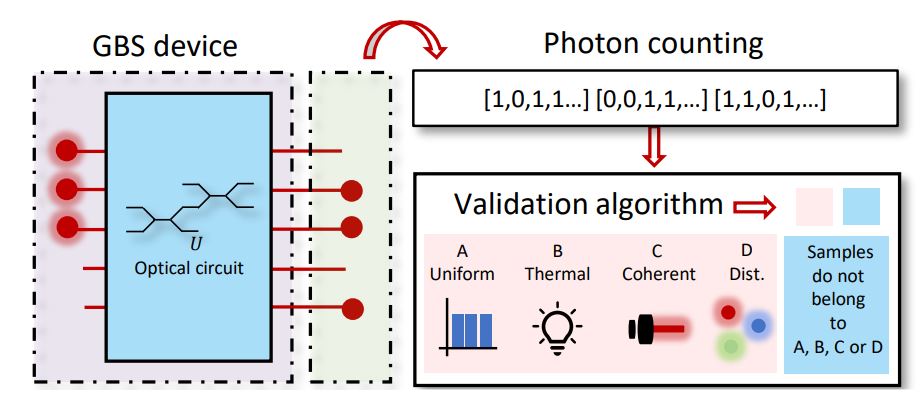
Gaussian Boson Sampling is a non-universal model for quantum computing inspired by the original formulation of the Boson Sampling problem. Nowadays, it represents a paradigmatic quantum platform to reach the quantum advantage regime in a specific computational model. Indeed, thanks to the implementation in photonics-based processors, the latest Gaussian Boson Sampling experiments have reached a level of complexity where the quantum apparatus has solved the task faster than currently up-to-date classical strategies. In addition, recent studies have identified possible applications beyond the inherent sampling task. In particular, a direct connection between photon counting of a genuine Gaussian Boson Sampling device and the number of perfect matchings in a graph has been established. In this work, we propose to exploit such a connection to benchmark Gaussian Boson Sampling experiments. We interpret the properties of the feature vectors of the graph encoded in the device as a signature of correct sampling from the true input state. Within this framework, two approaches that exploit the distributions of graph feature vectors and graph kernels are presented. Our results provide a novel approach to the actual need for tailored algorithms to benchmark large-scale Gaussian Boson Samplers.
Certification of Gaussian Boson Sampling via graph theory